Rules of the Coinche
Here you can find the rules of Coinche belote. Test your skills and play iBelote now.
The coinche is played between two teams of two players using a set of 32 classic cards (8 cards of each color - tile, clover, heart and spades).
La Coinche is a strategic game similar to the Bridge. In Coinche, players must evaluate their hands and estimate the number of points they think they can reach in the game. Players make contracts and the ads have a major role in the game.
How to play coinche:
- You need 4 players- Number of cards = 32
- End of the game, when one of the teams reaches 701 points.
The goal of the Coinche :
The goal of the game is to score more points than the opposing team. The winning team must realize the contract announced to win a round, and also realize at least 82 points of fold without announcement and belote-rebelote. The first team to reach a minimum of 701 points wins the game. In the case, both teams exceed 701 points, the one with the highest score wins the game.Value and order of cards at the Coinche:
At the coinche, the contract determines the value of the cards. For the color of the active the strongest card is Jack, the 3 other colors have identical value. If the player chooses All Trump (AT) or No Trump (NT), all the colors of the cards have the same vaues, for AT with the strongest card Jack and for NT with the strongest Ace card.| Trump | No Trump |
| Jack : 20 points | Ace : 11 points |
| 9 : 14 points | 10 : 10 points |
| Ace : 11 points | King : 4 points |
| 10 : 10 points | Queen : 3 points |
| King : 4 points | Jack : 2 points |
| Queen : 3 points | 9 : 0 point |
| 8 : 0 point | 8 : 0 point |
| 7 : 0 point | 7 : 0 point |
The distribution of cards :
On iBelote.com maps are distributed automatically. They are thrown in a counterclockwise direction. At La Coinche, all cards are dealt at the beginning of the round. Each player received 8 cards, 3 first cards then 2 then 3.Auctions :
The player to the left of the dealer starts. He can either pass his turn or announce a contract according to his cards. Once the player has announced a contract or has passed the nex player may announce a higher contract or pass. No advertised contract can be canceled. The team having announced the highest contract determines the color of the trump. The auction ends after 3 consecutive "Passes" if you have announced one of the players or if all players have announced passes in the first round. The last announced contract wins and the game phase can begin.For the trump color player can choose between:
One of the four colors;
All trump (AT) - all colors are trump, no color stronger than others;
No trump (NT) - for all colors is applied rules for a color other than the asset, no color is greater than the others
After a first bid by one of the players, one of the opposing players may announce Coinche. This assumes that the player thinks that the opponent will not realize his contract. A surcoinche can be made by the team that announced the auction, if the opposite player announces Coinche and the team feels certain to realize the contract that it announces.
Announcement value
Some combinations of cards can earn you points. These are the ads and players must compare them when the game begins. Only the team with the strongest ad wins the points for this ad. A card can count only one ad at a time, with the exception of the belote. All possible ads are listed below from the most powerful to the lowest.The square
4 cards of the same height. The value of a square depends on its height:
4 Jacks: 200 Points
4 Nine: 150 Points
4 Ace: 100 Points
4 Ten: 100 Points
4 Kings: 100 Points
4 Queens: 100 Points
Note: A square of 100 points is stronger than one hundred.
The Hundred
5 cards that follow each other in the same color in the following order: 7 8 9 10 Jack Dame King As.Value: 100 points.The Fifty
4 cards in the same color. Value: 50 points.Tierce
3 cards of the same suit.Value: 20 points.Belote
It is the king and the queen of trumped together in the same hand. Value: 20 points.Contract
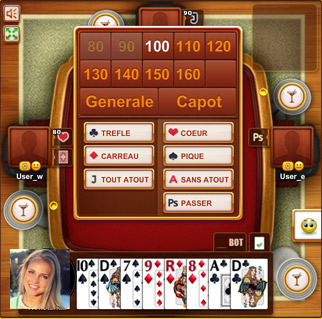
The team can make the contract according to the following types:- 80, 90,100,110 ... 160 points with trump color chosen. The team announces that the contract should reach a minimum of 82 points (10 of der is included) and also reach a minimum of points of contracts (80,90,100 etc.) with the help of Belote and other announcement.
- Capot with chosen trump color. The team should win all the folds. Hood have a value of 250 points
- Coinche of the last contract announced. Only for the players of the opposing team towards the player who announced the last contract. This announcement means that the player bet against the team that took the contract. In Coinche, the points are multiplied by 2
- General with asset color chosen. The player who took the contract must win all the folds himself. General have a value of 500 points
- Surcoinche - Only for the player who announced the last contract, or his partner. The team that makes the first contract may announce that the contract is still made (if the opposing team announces Coinche) with Recoinche.At Recoinche, the points are multiplied by 4.
How to count points at the Coinche ?
Each card gives points and the sum of all points are the final points for the team. The last fold is to add 10 extra points ("the 10 of der"). The final score is calculated on the basis of:- The team has completed its contract.
The team that realized its contract, obtains the points of the folds realized plus the points of the announced contract.
Example:
Team A announces 90 clubs and realizes its contract with 110 points then:
Team A = 90 + 110 = 200 points
Team B = 52 points
- If the team has not fulfilled its contract.
If the team that took the contract does not do it, it does not count points and then the opposing team gets 162 points plus all points of the announced contract.
Example:
Team A announces 140 clubs and achieves only 120 points:
Team A = 0 point
Team B = 162 + 120 = 282 points
Team A can only get Belote / Rebelote points, if they have.
- The case of the Hood or General. If the team announces the bonnet or General realizes it, the team gets all the points for the contract (250 for bonnet or 500 for General), in the other case the other team obtains points of the contract plus 162 points more plus announcement ( without belot)
- In case of Coinche or Surcoinche - If contract coined, same total x2 or in case of surcoinche, the points of the contract are multiplied by x4 (plus announcements)